Nadreálná čísla

Požadavky

Aby tato webová aplikace fungovala tak, jak má, potřebujete zařízení, které dovoluje kliknout a přetáhnout (počítačová myš, dotykový displej…). Mobilní zařízení doporučuji otočit na šířku.

Výklad této aplikace pochopí nejlépe ti, kteří mají znalosti matematiky alespoň středoškolské úrovně.

Co jsou nadreálná čísla?

Určitě znáš reálná čísla: -\(3\over7\), \(\sqrt{6^9}\), \(\pi\),… Nadreálná neboli Conwayova čísla obsahují všechna reálná čísla, ale i nekonečně velká čísla a čísla nekonečně malá. Než si ovšem řekneme, jak se konstruují, povíme si něco o historii jejich vzniku.

První definice nadreálných čísel vyplynula z výzkumu britského matematika Johna Hortona Conwaye, který jim ale tehdy říkal prostě čísla. Jméno nadreálná jim dal až v roce 1974 americký informatik Donald Ervin Knuth ve své noveletě, ve které pár studentů matematiky Alice a Bill na břehu Indického oceánu objevují kamennou desku s tajemnými nápisem. Společně pak prozkoumávají svět nadreálných čísel a postupně odkrývají jejich tajemství a zákonistosti.

Nyní se vydáme na podobnou cestu, na jejímž konci budeš nadreálná čísla znát skoro stejně dobře, jako Alice a Bill…

Definice nadreálných čísel

Nadreálné číslo \(x\) definujeme jako:
\[x = \lbrace X_L | X_R \rbrace, X_L \not\ge X_R\]

Hned je všechno jasné, že? Možná bude lepší přeložit matematické symboly do běžného jazyka…

Definice nadreálných čísel

\[x = \lbrace X_L | X_R \rbrace\]

Nadreálné číslo x je (uspořádaná) dvojice množin nadreálných čísel \(X_L\) a \(X_R\). Můžeš si to představit tak, že nadreálné číslo se skládá ze dvou "košů", do kterých se dávají další čísla. Která čísla jsou v koších pak určuje, jaké číslo vytvoří. Pozor, na pořadí košů záleží!

Množině \(X_L\) můžeme říkat taky levá množina daného čísla, množině \(X_R\) zase pravá množina.

Definice nadreálných čísel

\[X_L \not\ge X_R\]

Žádný prvek množiny \(X_L\) není větší ani roven žádnému prvku množiny \(X_R\). Čili všechny prvky množiny \(X_L\) jsou menší než všechny prvky množiny \(X_R\), neboli všechna čísla v levém "koši" jsou menší než všechna čísla v pravém "koši".

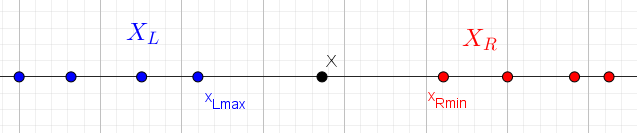
K porovnávání množin stačí porovnávat největší a nejmenší prvek každé množiny. Když \(x_{Lmax}\) je největší prvek množiny \(X_L\) a \(x_{Rmin}\) je nejmenší prvek množiny \(X_R\), tak např. \(x_{Lmax} \lt x_{Rmin} \iff X_L \lt X_R\) a tak dále pro všechna porovnání. Jinými slovy k porovnávání "košů" a čísel v nich stačí znát jen nejmenší a největší čísla.

Pseudo-čísla

Pokud bychom měli \(x = \lbrace X_L | X_R \rbrace\), ale \(X_L \ge X_R\), a tedy by byla porušena předchozí podmínka, x není nadreálné číslo, ale tzv. pseudo-číslo.

Pseudo-čísla jsou sice v jistém smyslu podobná číslům, ale nemají stejné všechny vlastnosti a chování.

Tvoření nadreálných čísel

Už jsme si řekli, že čísla, která jsou v levé a pravé množině, určují, jaké číslo z množiny vznikne. Ukážeme si teď základní vztah hledaného čísla a množin, ze kterých je tvořeno:

\[X_L \lt x \lt X_R\]

To znamená, že hledané číslo \(x\) je větší než všechna čísla v \(X_L\), ale menší než všechna čísla v \(X_R\). Bude tedy ležet někde mezi čísly z \(X_L\) a čísly z \(X_R\).

To nám napovídá první způsob, jak zkonstruovat kterékoli číslo \(\lbrace X_L | X_R \rbrace \): do množiny \(X_L\) dosadíme všechna (tj. všechna existující) čísla menší než \(x\) a do množiny \(X_R\) dosadíme všechna (tj. všechna existující) čísla větší než \(x\).

Tvoření nadreálných čísel

Ještě jednou se vrátím k metafoře s koši: k vytvoření nějakého nadreálného čísla \(x\) potřebujeme dva "koše" a do nich dáme nadreálná čísla. Jenže tato čísla musíme také nějak vytvořit, a k tomu potřebujeme další "koše" a další čísla, která také…

Vypadá to, jako bychom bloudili v kruhu. Ovšem řešení je prosté! Nadreálné číslo totiž můžeme zkonstruovat ze všech čísel, která jsme už vytvořili, i když jsme zatím nevytvořili žádná. Své první číslo zkonstruujeme ze dvou prázdných "košů", prázdných množin.

\[x = \lbrace \emptyset | \emptyset \rbrace = 0\]

Terminologická poznámka

Viděli jsme, že nadreálné číslo \(x = \lbrace \emptyset | \emptyset \rbrace\) se rovná dobře známému číslu \(x=0\). Tedy \(x\) je pořád to samé číslo, které ale má dvě různé reprezentace, \(\lbrace \emptyset | \emptyset \rbrace\) a \(0\). Aby se nepletly, budu občas mluvit o tvaru a hodnotě nadreálného čísla. Např. hodnotou čísla \(\lbrace \emptyset | \emptyset \rbrace\) je \(0\) a jedním z tvarů čísla \(0\) je \(\lbrace \emptyset | \emptyset \rbrace\)

Tvar čísla \(\lbrace \lbrace x_1; x_2; x_3 \rbrace | \lbrace x_4; x_5; x_6 \rbrace \rbrace\) se také zjednodušeně zapisuje jako \(\lbrace x_1; x_2; x_3 | x_4; x_5; x_6 \rbrace\). Znak svislé čáry | rozděluje danou uspořádanou množinu na příslušné dvě podmnožiny; všechna čísla nalevo od svislé čáry patří do levé množiny čísla a všechna čísla napravo patří do pravé množiny čísla.

Ovládání widgetů

Pro praktickou ukázku počítání s nadreálnými čísly budeme používat takovéto malé widgety:

Widget představuje takovou malou kalkulačku, vzorec k výpočtu s volnými poly pro zadání (nahoře vlevo), pole pro případný výsledek (nahoře vpravo) a možné hodnoty k zadání (dole). Zadávání do vzorce probíhá následovně:

• Klepni a přetáhni zvolené hodnoty na příslušná místa ve vzorci.
• Když přetáhneš hodnotu na místo, kde už je jiná hodnota, ta nová nahradí tu starou.
• Pokud chceš z pole odstranit již zadanou hodnotu, dvakrát na ni poklepej.
• Když vyplníš všechna pole ve vzorci, widget se automaticky pokusí vypočítat výsledek.
• • Pokud se výpočet podaří, zobrazí výsledek v poli pro výsledek.
  • Pokud při výpočtu narazí na nějakou chybu, oznámí to červená textová bublina.
• Výslednou hodnotu můžeš přidat do možností zadávaných hodnot tím, že klikneš na pole s výsledkem.
• • Jednotlivé widgety mohou omezovat, které hodnoty lze přidat do možností.
• Pokud budeš chtít odstranit nějakou hodnotu z možností, opět na ni můžeš dvakrát poklepat.

• Jak toho budeme o nadreálných číslech poznávat víc, budou přibývat i další možnosti zadávání.

• • Většinou si ale stačí pamatovat, že kliknutí na tlačítko přidá novou hodnotu do možností zadání.

Tvoření dalších čísel

Teď, když jsme si k prázdné množině vytvořili první nadreálné číslo, můžeme začít konstruovat další: \(\lbrace \emptyset | 0 \rbrace\) a \(\lbrace 0 | \emptyset \rbrace\) (\(\lbrace 0 | 0 \rbrace\) není nadreálné číslo, ale pseudo-číslo!) Zkus si to:

Tvoření dalších čísel

Výborně! Už máme 0, 1 a -1. Jaká další čísla ještě dokážeš vytvořit?

Tentokrát si můžeš kterýkoli výsledek přidat mezi možné zadávané hodnoty!

Genealogie nadreálných čísel

Všimni si, jak množina konstruovaných nadreálných čísel postupně roste: v prvním kroku jsme vytvořili jen 0, v dalším kroku přibyla -1 a 1 z nich jsme v dalším kroku udělali -2, -\(1 \over 2\), \(1 \over 2\) a 2… Vidíš? Nadreálná čísla se "rodí" v generacích. Generace je množina všech číslech, která vznikla ve stejném kroku.

Každou generaci můžeme očíslovat: první byla generace 0, pak generace 1, poté generace 2… Přitom platí, že číslo generace je stejné jako hodnota největšího nadreálného čísla \(x_{max}\) dané generace: v generaci 0 bylo největší číslo \(x_{max} = 0\), v generaci  bylo největší číslo \(x_{max} = 1\)…

Genealogie nadreálných čísel

Místo o generacích můžeme taky mluvit o narozeninách, resp. narozeninových číslech. Narozeninové číslo nadreálného čísla \(x\), matematicky zapsané jako \(\delta(x)\), je číslo generace, ve které se číslo \(x\) poprvé objevilo, a tedy největší nadreálné číslo ze stejné generace jako \(x\). Všechna čísla dané generace mají stejná narozeninová čísla: \(\delta(0) = 0\), \(\delta(-1) = \delta(1) = 1\), \(\delta(-2) = … = \delta(2) = 2\) a tak dále.

Některá nadreálná čísla mají narozeniny dříve a jiná později. Číslo \(x\) je mladší než \(y\), když \(\delta(x) \lt \delta(y)\), starší když \(\delta(x) \gt \delta(y)\) a stejně staré, když \(\delta(x) = \delta(y)\). V množinách také můžeme hledat, které číslo je nejstarší (nejdříve narozené, \(\delta(x)_{min}\)) anebo nejmladší (nejpozději narozené, \(\delta(x)_{max}\)).

Genealogie nadreálných čísel

Podívejme se ještě jednou, jak roste množina už vytvořených čísel: po prvním kroku obsahuje jen 0, v druhém -1, 0 a 1, ve třetím -2, -1, -\(1 \over 2\), 0, \(1 \over 2\) 1 a 2… Do každé generace \(\delta\) se narodí \(2^\delta\) čísel, takže po každém kroku (generaci \(\delta\)) máme celkem \(2^{\delta + 1} - 1\) nadreálných čísel.

Když seřadíme všechna dosud vytvořená čísla \(x_1\) \(\lt\) \(x_2\) \(\lt\) … \(\lt\) \(x_n\), po dalším kroku se všechna nová čísla zařadí takto mezi ně: \(\lbrace \emptyset|x_1 \rbrace\) \(\lt\) \(x_1\) \(\lt\) \(\lbrace x_1|x_2 \rbrace\) \(\lt\) \(x_2\) \(\lt\) \(\lbrace x_2|x_3 \rbrace\) \(\lt\) … \(\lt\) \(\lbrace x_{n-1}|x_n \rbrace\) \(\lt\) \(x_n\) \(\lt\) \(\lbrace x_n|\emptyset \rbrace\). Mezi každými dvěma původními čísly \(x_{i}\) a \(x_{i+1}\) se nachází nové číslo, které má tvar \(\lbrace x_{i}|x_{i+1} \rbrace\) a každé původní číslo \(x_{i}\) je obklopeno novými čísly (zleva i zprava právě jedním) ve tvaru \(\lbrace x_{i-1}|x_{i} \rbrace\) a \(\lbrace x_{i}|x_{i+1} \rbrace\) (za \(x_{-1}\) a \(x_{n+1}\) dosaď \(\emptyset\)). Nová čísla tedy zaplňují volný prostor a mezery mezi těmi původními.

Kanonický tvar nadreálných čísel

Zkus zjistit, jakou hodnotu mají čísla \(\lbrace -1|1 \rbrace\), \(\lbrace -2|2 \rbrace\),…

Kanonický tvar nadreálných čísel

Na předchozí straně sis mohl/a vyzkoušet, že číslo s hodnotou 0 může mít více různých tvarů. Platí to o každém nadreálném číslu, totiž že ho lze zapsat nekonečně mnoho ekvivalentními způsoby. Na těchto stránkách většinou, pokud není řečeno jinak, používáme ⁠⁠⁠⁠⁠tzv. kanonický tvar.

Kanonický tvar čísla \(x = \lbrace X_L | X_R \rbrace\) je takový, že ze všech možných \(x_L\) a \(x_R\) vybereme buď \(\emptyset\), nebo to číslo, které je nejstarší (neboli které má mezi všemi možnými čísly nejmenší narozeninové číslo \(\delta\)). Zároveň je to ten tvar, ve kterém bylo dané číslo poprvé vytvořeno.

Např. číslo 1 můžeme zapsat ve tvarech: \(\lbrace 0|\emptyset \rbrace\), \(\lbrace {1 \over 2}|2 \rbrace\), \(\lbrace {3 \over 4}|{5 \over 4} \rbrace\)… Kanonický tvar čísla 1 je ale jen ten první, \(\lbrace 0|\emptyset \rbrace\).

Stromová struktura nadreálných čísel

Když napíšeš pod sebe jednotlivé po sobě jdoucí generace nadreálných čísel tak, aby když \(x_1 \lt x_2\) bylo \(x_1\) vlevo od \(x_2\), vznikne ti určitá stromová struktura nadreálných čísel:

Vytvořil Lukáš Lánský, CC BY-SA 3.0, Odkaz na původní obrázek

Stromová struktura nadreálných čísel

Této struktuře se v informatice říká binární vyhledávací strom.

Strom představuje strukturu propojených prvků, kde každý prvek má jednoho přímého předka (nebo žádného, viz číslo 0; takovému prvku se říká kořen a každý strom má právě jeden) a určitý počet přímých potomků. Binární strom znamená, že každý prvek má až dva přímé potomky. U vyhledávacích binárních stromů rozlišujeme potomky nalevo a napravo, přičemž všichni potomci prvku \(x\) nalevo mají menší hodnotu než \(x\) a všichni potomci napravo mají větší hodnotu než \(x\). Nepřipomíná ti to něco?

\[X_L \lt x \lt X_R\]

To je přece jedna ze základních vlastností nadreálných čísel!

Terminologická poznámka 2

V definici binárního vyhledávacího stromu jsem zmínil, že každý prvek má (maximálně) jednoho přímého předka a až dva přímé potomky. Ovšem stejně jako se „předci“ neříká jen otci a matce a „potomci“ jen dcerám a synům, budou předci prvku znamenat množinu nejen přímého předka, ale i všech jeho předků; a potomci prvku budou znamenat množinu nejen přímých potomků, i všech jejich potomků. Potomci nalevo budou množina přímého potomka naleva a všech jeho potomků; potomci napravo budou množina přímého potomka napravo a všech jeho potomků.

Pokud nějaký prvek \(z\) je předkem prvku \(x\) a zároveň předkem prvku \(y\), říkáme mu společný předek prvků \(x\) a \(y\).

Stromová struktura nadreálných čísel

Podívej se ještě jednou na obrázek stromové struktury nadreálných čísel a všimni si, že díky tomu, jak jdou jednotlivé generace po sobě, pro každé číslo \(x\) platí, že všichni jeho potomci jsou mladší a všichni jeho předci jsou starší. Přičemž přímí potomci a přímý předek mají narozeninové číslo jen o 1 větší či menší než dané číslo \(x\).

Vytvořil Lukáš Lánský, CC BY-SA 3.0, Odkaz na původní obrázek

Výpočet konkrétní hodnoty nadreálného čísla

Možná tě napadla otázka: jak určit, že např. hodnota čísla \(\lbrace {1\over 4}|{7\over 8} \rbrace\) je právě \(1\over 2\) a ne třeba \(9\over 16\)? Pro číslo \( x = \lbrace x_L|x_R \rbrace\) platí, že \(x\) je nejstarší číslo takové, že \(x_L \lt x \lt x_R\). S nalezením takového čísla nám může pomoci stromová struktura nadreálných čísel. Stačí vzít čísla \(x_L\) a \(x_R\) a v prostoru mezi nimi vyhledat nejstarší číslo. Na tomto obrázku si to ukážeme na výše zmíněném příkladu \(\lbrace {1\over 4}|{7\over 8} \rbrace = {1\over 2}\):

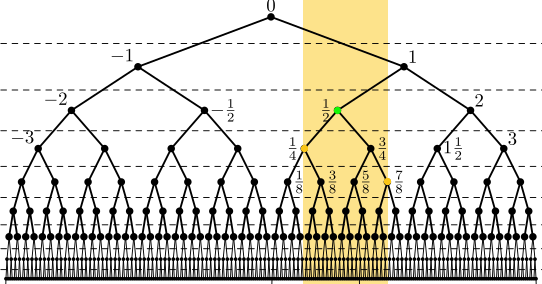
Upraveno, originál vytvořil Lukáš Lánský, CC BY-SA 3.0, Odkaz na původní obrázek

Výpočet konkrétní hodnoty nadreálného čísla

„Nejstarší číslo mezi dvěma čísly“ může být buď starší než \(x_L\) i \(x_R\) – potom bylo vytvořeno už v některé z předchozích generací – nebo mladší než \(x_L\) i \(x_R\) a musíme ho proto teprve zkonstruovat do následující generace. V takovém případě bude forma \(\lbrace x_L|x_R \rbrace\) kanonickou formou \(x\).

V tento moment máme čtyři možnosti vytvoření nového čísla. Zaprvé, triviální případ \(\lbrace \emptyset|\emptyset \rbrace\), tedy prostě „nejstarší číslo“. To už víme, že je 0. Zadruhé, \(\lbrace x_L|\emptyset \rbrace\), tedy „nejstarší číslo větší než \(x_L\)“, které vytvoříme jednoduše tím, že k \(x_L\) přičteme 1. Zatřetí, \(\lbrace \emptyset|x_R \rbrace\), „nejstarší číslo menší než \(x_R\)“ je obdobný případ jako ten předchozí, pouze od \(x_R\) odečteme 1. Např. \(\lbrace 5|\emptyset \rbrace = 6\) a \(\lbrace \emptyset|-9 \rbrace = -10\).

Konečně začtvrté, když ani jedno z \(x_L\) ani \(x_R\) není prázdná množina, ale obě jsou nějaká čísla, pak hodnota čísla \(x_L \lt x \lt x_R\) leží přesně mezi \(x_L\) a \(x_R\) a vypočítáme ji vzorcem \(x={x_L+x_R\over 2}\), např. \(\lbrace 5|6 \rbrace = {5+6\over 2} = {11\over 2}\).

Výpočet konkrétní hodnoty nadreálného čísla

Ještě než budeme pokračovat, mužeš si nově nabyté znalosti o konstrukci nadreálných čísel vyzkoušet prakticky. Obrázek stromové struktury nadreálných čísel můžeš využít jako nápovědu.

Vytvořil Lukáš Lánský, CC BY-SA 3.0, Odkaz na původní obrázek

Celá a dyadická čísla

Možná sis při testování konstrukce nadreálných čísel všimnul/a, že všechna konstruovaná čísla jsou buď celá, nebo zlomek se sudým jmenovatelem.

To kvůli způsobu, jakým nová čísla vytváříme: buď přičteme \(\pm 1\) – tak mohou vzniknout pouze celá čísla – nebo původní čísla sečteme a vydělíme 2 – tak vzniknou jen tzv. dyadické zlomky, tedy čísla ve tvaru \(a\over 2^b\), kde koeficienty \(a\) a \(b\) jsou celá čísla. Na úplném začátku jsem ale sliboval, že nadreálná čísla obsahují i všechna reálná čísla a ještě spousta dalších. Jak je zkonstruovat?

Vtip je v tom, že jsme zatím nadreálná čísla skládali pouze z konečných množin. Ale za \(X_L\) a \(X_R\) můžeme dosadit nekonečné množiny a posloupnosti…

Reálná čísla

Jak na reálná čísla? Pro reálné číslo \(r = \lbrace R_L | R_R \rbrace\) potřebujeme najít takové množiny dyadických zlomků \(R_L\) a \(R_R\), aby \(R_L \lt r \lt R_R\). Hledané dyadické zlomky budou členy dvou nekonečných posloupností: jedné, která se blíží k limitě \(r\) zdola (pro prvky \(R_L\)), a druhé, která se blíží k limitě \(r\) shora (pro prvky \(R_R\)). Tak například:

\[{1\over 3} = \lbrace \lbrace {1\over 4}; {5\over 16}; {21\over 64}; {85\over 256};\dots \rbrace | \lbrace {1\over 2}; {3\over 8}; {11\over 32}; {43\over 128};\dots \rbrace \rbrace \]

\[\pi = \lbrace \lbrace 3{,}125; 3{,}140625; 3{,}14111328125;\dots \rbrace | \lbrace 3{,}5; 3{,}25; 3{,}1875; 3{,}15625;\dots \rbrace \rbrace \]

Za hranu nekonečna

Co když nekonečná řada nekonverguje, ale roste nebo klesá do nekonečna? Existuje třeba číslo \(x =\lbrace \lbrace 1; 2; 3; 4;\dots \rbrace | \emptyset \rbrace \)? Ano, je to „číslo větší než všechna reálná čísla“. Hodnotu takového čísla samozřejmě nelze vyjádřit jakýmkoli reálným číslem, proto zavedeme novou transfinitní „jednotku“:

\[\lbrace \lbrace 1; 2; 3; 4;\dots \rbrace | \emptyset \rbrace = \omega\]

Obdobně \(\lbrace \emptyset | \lbrace -1; -2; -3; -4;\dots \rbrace \rbrace = -\omega\). Ovšem pokud bychom konstruovali nadreálná čísla postupně od 0, k \(\pm\omega\) bychom se dostali až po nekonečně mnoha krocích! Naštěstí jsem si pro tebe pár nekonečných množin připravil dopředu:

Za hranu nekonečna

Podobně jako první číslo 0 umožnilo konstruovat další a další čísla, s prvními transfinitními čísly \(\pm\omega\) můžeme konstruovat další a další transfinitní čísla (transfinitní znamená „za konečnem“, „za“ všemi konečnými čísly).

Lze vytvořit třeba „čísla větší než \(\omega\)“ \(\lbrace \omega | \emptyset \rbrace = \omega + 1\), \(\lbrace \omega + 1| \emptyset \rbrace = \omega + 2\)… a „čísla menší než \(-\omega\)“ \(\lbrace \emptyset | -\omega \rbrace = -\omega - 1\)…

Za hranu nekonečna

Jak vytvořit čísla jako \(\omega - 1\), \(-\omega + 2\)…? Nestačí „číslo menší než \(\omega\)“, protože \(\lbrace \emptyset | \omega \rbrace\) je 0…

Tak například \(\omega - 1 = \lbrace \lbrace 1; 2; 3;\dots \rbrace | \omega \rbrace\), čili „číslo větší než všechna reálná čísla, ale menší než \(\omega\)“. Podobně \(-\omega+1 = \lbrace -\omega | \lbrace -1; -2; -3;\dots \rbrace \rbrace\), čili „číslo větší než \(-\omega\), ale menší než všechna reálná čísla“ a dále \(-\omega+2 = \lbrace -\omega+1 | \lbrace -1; -2; -3;\dots \rbrace \rbrace\), \(\omega-3 = \lbrace \lbrace 1; 2; 3;\dots \rbrace | \omega - 2 \rbrace\) apod.

Za hranu nekonečna

Při skládání transfinitních čísel se jejich reálné části chovají funguje podobně stejně jako u konečných čísel, např. \(\lbrace \omega + 1|\omega + 2 \rbrace = \omega+{3\over 2}\). Tady máš příležitost si vyzkoušet, co ses o transfinitních číslech doposud naučil:

Za hranu nekonečna

Jako jsme nechali divergovat do nekonečna množinu reálných čísel, můžeme použít i množiny jako \(\lbrace \omega+1; \omega+2; \omega+3;\dots \rbrace\):

\[\lbrace \lbrace \omega+1; \omega+2; \omega+3;\dots \rbrace | \emptyset \rbrace = 2\omega\]

\[\lbrace \lbrace 1; 2; 3;\dots \rbrace \rbrace | \lbrace \omega-1; \omega-2; \omega-3;\dots \rbrace \rbrace = {1\over 2}\omega\]

\[\lbrace \emptyset | \lbrace -\omega-1; -\omega-2; -\omega-3;\dots \rbrace \rbrace = -2\omega\]

\[\lbrace \lbrace -\omega+1; -\omega+2; -\omega+3;\dots \rbrace \rbrace | \lbrace -1; -2; -3;\dots \rbrace \rbrace = -{1\over 2}\omega\]

Za hranu nekonečna

Asi už tušíš, že \(\lbrace \lbrace 2\omega+1; 2\omega+2; 2\omega+3;\dots \rbrace | \emptyset \rbrace\) bude \(3\omega\) atd. Při vytváření \({3\over 2}\omega\) si musíš dát pozor, že \(\lbrace \omega | 2\omega \rbrace = \omega+1\) a \(\lbrace \lbrace \omega+1; \omega+2; \omega+3;\dots \rbrace | 2\omega \rbrace = 2\omega-1\), takže až \(\lbrace \lbrace \omega+1; \omega+2; \omega+3;\dots \rbrace | \lbrace 2\omega-1; 2\omega-2; 2\omega-3;\dots \rbrace \rbrace = {3\over 2}\omega\).

Jinak se ale i transfinitní čísla chovají dost podobně jako reálná, takže ti nic nebrání zkonstruovat si třeba \(-{9\over 16}\omega + 420\).

Dokonce i transfinitní čísla mají svá narozeninové čísla. Takže \(\delta(\omega)\) a \(\delta(-\omega)\) \(=\omega\), protože \(\omega\) je největší číslo dané generace. Další generace pak mají narozeninová čísla \(\omega+1\), \(\omega+2\)… Mimochodem, \(\omega\) je narozeninové číslo i všech nedyadických reálných čísel jako \(1\over 3\), protože i na jejich vytvoření potřebuješ nekonečně mnoho kroků, nekonečně mnoho generací. Narozeninové číslo \(\delta(2\omega)\) je nepřekvapivě \(2\omega\), \(\delta(3\omega) = 3\omega\), \(\delta(3\omega + 2) = 3\omega + 2\)…

Za hranu nekonečna

Ještě si ukážeme, co s \(\lbrace \omega; 2\omega; 3\omega;\dots \rbrace\) a \(\lbrace \omega; {1\over 2}\omega; {1\over 3}\omega;\dots \rbrace\):

\[\lbrace \lbrace \omega; 2\omega; 3\omega;\dots \rbrace | \emptyset \rbrace = \omega^2\]

\[\lbrace \lbrace 1; 2; 3;\dots \rbrace | \lbrace \omega; {1\over 2}\omega; {1\over 3}\omega;\dots \rbrace \rbrace = \sqrt{\omega}\]

A stejně vznikne i \(-\omega^2\) a \(-\sqrt{\omega}\). Všechna tato čísla mají narozeninové číslo \(\omega^2\), vždyť \(\omega^2\) je největší číslo jejich generace. Mohli bychom zkoumat ještě \(\omega^3\), \(\omega^\omega\) a jiné, naše cesta už ovšem zase pomalu, ale jistě pokračuje k dalšímu druhu čísel…

Za hranu nekonečna

Přiznám se, že když jsem ti ukazoval stromovu strukturu nadreálných čísel, neukázal jsem ji celou. To hned napravím (mimochodem, obrázek obsahuje i čísla, kterými se budeme zabývat dál; schválně je zkus najít a zamyslet se, o co by mohlo jít):

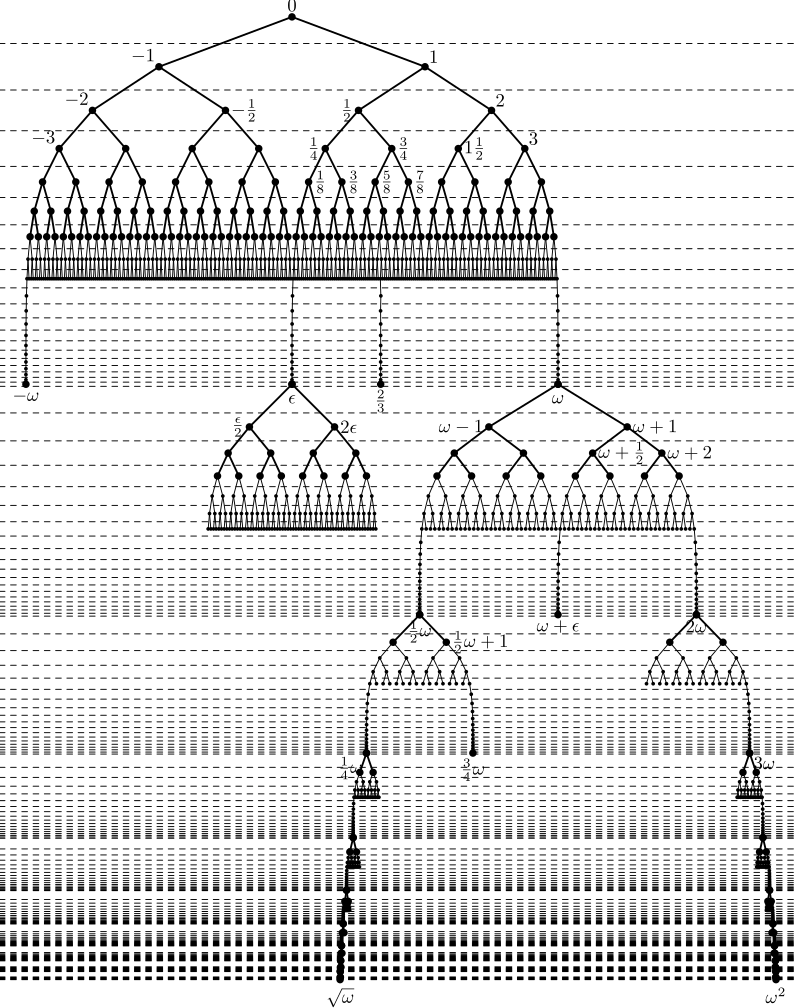
Vytvořil Lukáš Lánský, CC BY-SA 3.0, Odkaz na původní obrázek

Všimni si, že čísla jako \(\omega\), \(\epsilon\) a jejich násobky sice mají nekonečno předků, ale žádného přímého předka. Přímé předky má smysl rozlišovat jen u čísel, která (v kanonickém tvaru) vznikla z aspoň jedné konečné množiny (\(\emptyset\) se nepočítá).

Za hranu nekonečna

A zde máš kalkulačku, na které si můžeš ještě jednou vyzkoušet i práci s transfinitními čísly:

Infinitesimální čísla

Když máme čísla větší než všechna reálná čísla, můžeme mít i čísla „nekonečně malá“ (=infinitesimální), ve smyslu větší než 0, ale menší než všechna (kladná) dyadická čísla, když  si k jejich konstrukci pomůžeme nekonečnou množinou blížící se k limitě 0. Hodnotu takového čísla opět nelze vyjádřit jakýmkoli reálným číslem, proto zavedeme novou infinitesimální „jednotku“:

\[\lbrace 0 | \lbrace {1\over 2}; {1\over 4}; {1\over 8};\dots\rbrace \rbrace = \epsilon\]

\[\lbrace \lbrace -{1\over 2}; -{1\over 4}; -{1\over 8};\dots\rbrace | 0 \rbrace = -\epsilon\]

Infinitesimální čísla

Číslo \(\epsilon\) je „větší než 0 ale menší než všechna kladná dyadická čísla“. Všimni si, že čísla se k 0 můžou blížit zprava od kladných čísel i zleva od záporných čísel. Nekonečná množina, ze které skládáme infinitesimální čísla, se nemusí blížit jen k limitě 0, ale ke kterémukoli číslu, takže můžeš vytvořit třeba \(1-\epsilon\), \(-{1\over 4}+\epsilon\) a později i \({2\over 3}-\epsilon\) či \(\omega+\epsilon\).

\[1-\epsilon = \lbrace \lbrace 1-{1\over 2}; 1-{1\over 4}; 1-{1\over 8};\dots\rbrace | 1 \rbrace\]

\[\omega+\epsilon = \lbrace \omega | \lbrace \omega+{1\over 2}; \omega+{1\over 4}; \omega+{1\over 8};\dots\rbrace \rbrace\]

Číslo \(\epsilon\) patří do stejné generace jako \(\omega\), tedy narozeninová čísla \(\delta(\epsilon)=\delta(\omega)=\omega\). Stejně tak \(1-\epsilon\), \(-{1\over 4}+\epsilon\), ale \({2\over 3}-\epsilon\) a \(\omega+\epsilon\) mají narozeniny až ve \(2\omega\) (protože nejdřív se nekonečno generací dostáváš k \(2\over 3\) či \(\omega\), a pak ještě druhých nekonečno generací k \(\epsilon\)).

Infinitesimální čísla

Podobně jako jsme mohli dále pracovat s \(\omega\), můžeme použít infinitesimální čísla ke konstrukci dalších čísel. Mezi 0 a \(\epsilon\) nalezneme \({1\over 2}\epsilon = \lbrace 0 | \epsilon\rbrace\), mezi \(\epsilon\) a všemi většími reálnými čísly \(2\epsilon = \lbrace \epsilon | \lbrace {1\over 2}; {1\over 4}; {1\over 8};\dots\rbrace\rbrace\) a podobně \(-{1\over 2}\epsilon = \lbrace -\epsilon|0 \rbrace\), \(-2\epsilon = \lbrace \lbrace -{1\over 2}; -{1\over 4}; -{1\over 8};\dots\rbrace | \epsilon \rbrace\), \(1+{1\over 2}\epsilon = \lbrace 1 | 1+\epsilon\rbrace\), \({1\over 4}\epsilon = \lbrace 0 | {1\over 2}\epsilon\rbrace\), \({3\over 4}\epsilon = \lbrace \epsilon | 2\epsilon\rbrace\) a tak dále. Ještě jednou si to prohlédni na dobře známém obrázku:

Vytvořil Lukáš Lánský, CC BY-SA 3.0, Odkaz na původní obrázek

Infinitesimální čísla

Už jsme se skoro na konci povídání o konstrukci nadreálných čísel, jen mi ještě dovol doplnit, co vznikne z nekonečných množin infinitesimálních čísel:

\[\lbrace 0 | \lbrace {1\over 2}\epsilon; {1\over 4}\epsilon; {1\over 8}\epsilon;\dots\rbrace \rbrace = \epsilon^2\]

\[\lbrace \lbrace \epsilon; 2\epsilon; 3\epsilon;\dots\rbrace | \lbrace {1\over 2}; {1\over 4}; {1\over 8};\dots\rbrace \rbrace = \sqrt{\epsilon}\]

A stejně vznikne třeba i \(1-\epsilon^2\) a \(-2-\sqrt{\epsilon}\). Všechna tato čísla patří do stejné generace jako \(\omega^2\), takže jejich narozeninové číslo \(\delta\) je také \(\omega^2\).

Kalkulačka konstrukce nadreálných čísel

Teď když znáš všechna možná nadreálná čísla si můžeš opět zkusit jejich konstrukci. Máš poslední příležitost, dál totiž budeme probírat operace s nadreálnými čísly.

Porovnávání nadreálných čísel

Nadreálná čísla jsou největší úplně uspořádanou množinou. Úplně uspořádaná množina je taková, na které je definována úplná binární relace uspořádání, resp. jejíž každé dva prvky můžeme porovnat. Nadreálná čísla obsahují všechny takové množiny a všechna taková čísla.

Porovnání je pro nadreálná čísla naprosto zásadní, proto se pojďme podívat na jeho definici:

\[x \le y \iff X_L \not\ge y \land x \not\ge Y_R\]

Když si uvědomíme, že \(\not\ge\) je to samé jako \(\lt\), můžeme nerovnici přepsat na trochu srozumitelnější:

\[x \le y \iff X_L \lt y \land x \lt Y_R\]

Jinými slovy \(x\) je menší nebo rovno \(y\) právě tehdy, když všechna čísla množiny \(X_L\) jsou menší než \(y\) a \(x\) je menší než všechna čísla množiny \(Y_R\). Názorně si to ukážeme na tomto obrázku:

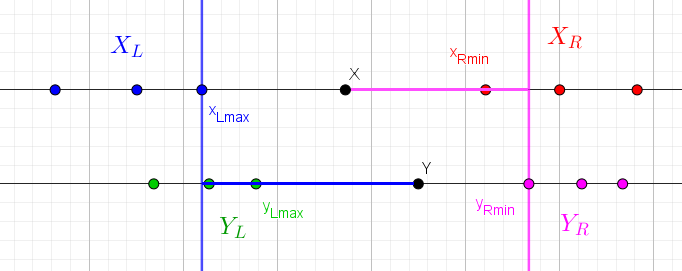
Porovnání \(x\ge y\) můžeme napsat jako \(y \le x\), s čímž si už poradíme předchozím vzorcem. Zbylá porovnání získáme kombinací těch, co jsme právě popsali, a logické negace (není větší než, není větší než…)

Sčítání nadreálných čísel

Sčítání je operace se dvěma nadreálnými čísly \(x\) a \(y\), kterou definujeme následovně:

\(x + y = \lbrace X_L | X_R \rbrace + \lbrace Y_L | Y_R \rbrace\)\( = \lbrace X_L+y \cup x+Y_L | X_R+y \cup x+Y_R \rbrace\).

Aby nedošlo k nedorozumění: sjednocujeme vždy výsledky dílčích operací, tedy \(X_L+y \cup x+Y_L\)\(= \lbrace X_L+y \rbrace \cup \lbrace x+Y_L \rbrace\) atd. Čili vzorec sčítání znamená, že ke všem prvkům levé množiny \(x\) přičteme číslo \(y\) a k číslu \(x\) přičteme všechny prvky levé množiny \(y\), dáme všechny tyto výsledky do jedné množiny a to bude výsledná levá množina. Stejně tak přičteme čísla k prvkům pravých množin a z nich vytvoříme výslednou pravou množinu. Ještě doplním, že výsledkem sčítání s prázdnou množinou je zase prázdná množina (nemáme totiž žádné prvky ke sčítání, takže ani žádné další nevzniknou).

Příklad: \({3\over 2} + {1\over 2} = \lbrace 1|2 \rbrace + \lbrace 0|1 \rbrace\)\(=\lbrace 1+{1\over 2} \cup {3\over 2}+0|2+{1\over 2}\cup{3\over 2}+2\rbrace\) \(=\lbrace{3\over 2}|{5\over 2}, {7\over 2}\rbrace=2\)

Sčítání nadreálných čísel

Sčítání nadreálných čísel má stejné chování a vlastnosti jako sčítání reálných čísel: je asociativní (\(a+(b+c)=(a+b)+c=a+b+c\)), komutativní (\(a+b=b+a\)) a má neutrální prvek 0 (\(a+0=a\)).

Při sčítání tedy sice nezáleží na pořadí, takže můžeš provést \(Y_L+x\) místo \(x+Y_L\), přesto si toto pořadí ve vzorcích pamatuj, protože bude hrát roli při odčítání.

Negace nadreálných čísel

Negace nadreálného čísla neboli číslo opačné je velice jednoduchou operací:

\[-x = \lbrace -X_R | -X_L \rbrace\]

Tedy prohodíme levou a pravou množinu a všechna čísla v nich vynásobíme -1, takže se obrátí jejich pořadí.

Příklad: \(-({5\over 2}) = -\lbrace 2|3\rbrace = \lbrace -3|-2\rbrace = -{5\over 2}\)

Odčítání nadreálných čísel

Operaci odčítání definujeme pomocí sčítání a negace:

\(x - y = x +(-y)\)

Číslo \(y\) tedy nejdřív zneguješ a pak přičteš k číslu \(x\), což rozepsané podle vzorců vypadá takto:

\(x - y\)\(= \lbrace X_L+(-y) \cup x+(-Y_R) | X_R+(-y) \cup x+(-Y_L) \rbrace\)\(= \lbrace X_L-y \cup x-Y_R | X_R-y \cup x-Y_L \rbrace\)

Neboli odčítání provádíme podobně jako sčítání, jen vyměníme množiny \(Y_L\) a \(Y_R\) a místo operace sčítání odčítáme.

Příklad: \({3\over 2} - {1\over 2} = \lbrace 1|2 \rbrace - \lbrace 0|1 \rbrace\)\(= \lbrace 1|2 \rbrace + \lbrace -1|0 \rbrace\)\(=\lbrace 1-{1\over 2} \cup {3\over 2}-1|2-{1\over 2}\cup{3\over 2}-0\rbrace\) \(=\lbrace{1\over 2}|{3\over 2}\rbrace=1\)

Kalkulačka sčítání a odčítání

Nově objevené operace si vyzkoušej a zkontroluj s výsledky této kalkulačky:

Násobení nadreálných čísel

Operace násobení dvou nadreálných čísel definujeme poměrně složitě:

\(xy = \lbrace X_Ly + xY_L - X_L Y_L \cup X_Ry + xY_R - X_R Y_R | X_Ly + xY_R - X_L Y_R \cup X_Ry + xY_L - X_R Y_L \rbrace\)

kde např. \(X_Ny\) znamená vynásobení všech prvků množiny \(X_N\) číslem \(y\) a \(X_N Y_M\) znamená roznásobení všech prvků množiny \(X_N\) se všemi prvky množiny \(Y_M\). Ze všech takových kombinací pak vznikne množina, z níž se skládá výsledné nadreálné číslo. Všimni si, že se ve vzorci několikrát opakuje ten samý postup \(X_Ny + xY_N - X_N Y_N\), jen se mění kombinace L a R; v levé množině výsledného čísla jsou vždy podobné (\(LL\) a \(RR\)), v pravé vždy opačné (\(LR\) a \(RL\)). Pokud je kterákoli z množin \(\emptyset\), výsledkem je také prázdná množina \(\emptyset\).

Násobení nadreálných čísel

Jakkoli je násobení složitě definováno, funguje ve výsledku stejně jako známé násobení reálných čísel a má i stejnéné vlastnosti: je asociativní (\(a(bc)=(ab)c=abc\)), komutativní (\(ab=ba\)), distributivní (\(a(b+c) = ab+ac\)), má neutrální prvek 1 (\(1a=1\)) a absorbující prvek 0 (\(0a=0\)).

Aby ses s násobením příliš nenadřel/a, dám ti kalkulačku i na násobení nadreálných čísel:

Vztah \(\omega\) a \(\epsilon\)

Když už máme definované násobení, má smysl si ukázat ještě jeden speciální vztah mezi \(\omega\) a \(\epsilon\):

\[\omega^n\epsilon^n = \omega^0\epsilon^0 = 1\]

\(\epsilon = {1\over \omega} = \omega^{-1}\)\(\qquad\)\(\omega = {1\over \epsilon} = \epsilon^{-1}\)

\(\epsilon^2 = {1\over \omega^2} = \omega^{-2}\)\(\qquad\)\(\omega^2 = {1\over \epsilon^2} = \epsilon^{-2}\)

\(\sqrt{\epsilon} = {1\over \sqrt{\omega}} = \omega^{-{1\over 2}}\)\(\qquad\)\(\sqrt{\omega} = {1\over \sqrt{\epsilon}} = \epsilon^{-{1\over 2}}\)

Hodnotu čísla \(\omega^2 + \omega + \sqrt{\omega} + 1 + \sqrt{\epsilon} + \epsilon + \epsilon^2\) můžeme zapsat jako \(\omega^2 + \omega + \omega^{1\over 2} + 1 + \omega^{-{1\over 2}} + \omega^{-1} + \omega^{-2}\).

Nadkomplexní čísla

Stejně jako komplexní čísla vznikají rozšířením reálných čísel zavedením imaginární jednotky \(i\), můžeme definovat nadkomplexní čísla jako číslo ve tvaru

\[x = a + bi\]

kde \(a\) a \(b\) jsou nadreálné koeficienty a \(i\) je imaginární jednotka.

Využití v teorii her

Nadreálná čísla jsou spíše matematickou hračkou pro zábavu a zajímavost, najdou však i své využití, např. v teorii her.

Představme si hru mezi dvěma hráči L a P. Můžou jí být klidně třeba šachy nebo čínská desková hra Go (koneckonců právě díky výzkumu konců hry Go byla nadreálná čísla vynalezena), každá hra ale musí splňovat toto zadání:

• hra musí být deterministická (nesmí v ní hrát roli náhoda),
• nesmí osahovat skryté informace (hráči si takříkajíc musí „vidět do karet“),
• hráči se musí střídat (nemohou najednou zahrát vícero tahů),
• hráč prohrává, když  už nemůže udělat žádný platný tah (podle pravidel).

Využití v teorii her

V některých postaveních hry mívá jeden z hráčů výhodu. Hodilo by se nějakým způsobem přiřadit každé hře určitou hodnotu, určité číslo. Proto definujeme postavení neboli hru \(H = \lbrace L | P \rbrace\), kde \(L\) je množina tahů, které v dané pozici může udělat hráč L, tedy množina všech postavení, do kterých se může hra dostat jedním tahem hráče L; \(P\) je obdobná množina tahů hráče P.

Pokud ti tento zápis nic nepřipomíná, zopakuj si všechno pěkně od začátku. Narozdíl od nadreálných čísel ale hry můžou tvořit i množiny \(L\) a \(P\), pro které neplatí \(L \lt P\) (tedy hrou může být nadreálné číslo i pseudo-číslo).

Využití v teorii her

Jak už bylo řečeno, hráč prohrává, když už nemůže udělat žádný platný tah: Když \(H = \lbrace \emptyset | \emptyset \rbrace\), není v daném postavení k dispozici žádný platný tah, takže hráč, který je další na řadě, nemůže nic dělat a prohraje. Hru \(H = \lbrace 0 | \emptyset \rbrace\) vyhraje hráč L, ať už je na řadě kdokoli, hru \(H = \lbrace \emptyset | 0 \rbrace\) zase určitě vyhraje hráč P a hru \(H = \lbrace 0 | 0 \rbrace\) vyhraje ten hráč, který je další na řadě.

Pokud budeme předpokládat dokonalé hráče, kteří nedělají chyby, lze tato pravidla zobecnit podle porovnání hodnoty \(H\): \(H = 0\) (ten, kdo je další na řadě, prohraje), \(H \gt 0\) (vyhraje hráč L), \(H \lt 0\) (vyhraje hráč P) a \(H \lVert 0\) (ten, kdo je další na řadě, prohraje; kde \(H\) je pseudo-číslo nesrovnatelné s 0).

Některé hry lze rozdělit na nezávislé menší hry \(G\) a \(H\), které můžeme zanalyzovat samostatně a celkovou hru pak popsat jako \(G+H\). Právě to bylo původní motivací Johna Conwaye, která ho zavedla až k nadreálným číslům. Poněkud poeticky tak můžeme říct, že skončíme tam, kde on začal.

Navigace

1. Požadavky
2. Co jsou nadreálná čísla?
3. Definice
4. Pseudo-čísla
5. Tvoření nadreálných čísel
6. Ovládání widgetů
7. Tvoření dalších čísel
8. Genealogie nadreálných čísel
9. Kanonický tvar
10. Stromová struktura
11. Výpočet konkrétní hodnoty
12. Celá a dyadická čísla
13. Reálná čísla
14. Za hranu nekonečna
15. Infinitesimální čísla
16. Kalkulačka konstrukce nadreálných čísel
17. Porovnávání konstrukce nadreálných čísel
18. Sčítání nadreálných čísel
19. Negace nadreálných čísel
20. Odčítání nadreálných čísel
21. Kalkulačka sčítání a odčítání
22. Násobení nadreálných čísel
23. Vztah \(\omega\) a \(\epsilon\)
24. Nadkomplexní čísla
25. Využití v teorii her
26. Literatura k dalšímu studiu

Literatura k dalšímu studiu:

1. KNUTH, Donald Ervin: Surreal Numbers: How Two Ex-Students Turned On to Pure Mathematics and Found Total Happiness (do češtiny přeložila Hana Nešetřilová)
2. CONWAY, John Horton: On Numbers and Games
3. GONSHOR, Harry: An Introduction to the Theory of Surreal Numbers